
志鸿优化系列丛书 志鸿优化网,永远提供更新的! 丛书主编任志湖。 http://www.zhyh.org 2.2.2 直线的两点式方程 课后·训练提升 基础巩固 1.经过两点(5,0),(2,-5)的直线方程为( A.5x+3y-25=0 B.5x-3y-25=0 C.3x-51-25=0 D.5x-3y+25=0 答案B 解析经过两点(5,0),(2,-5)的直线方程为 品=器整理得5x-3-25-0 故选B. 2.已知直线1ar+y-2=0在x轴和y轴上的截距相等,则实数a的值是() A.1 B.-1 C.-2或-1 D.-2或1 含案]A 解标显然a0.把直线1+2=-0化为艺+=l. 因为直线1:ar+y-2=0在x轴和y轴上的截距相等, 所以2=2,解得a=1,故选A 3.若一条直线不与坐标轴平行或重合,则它的方程() A.可以写成两点式或截距式 B.可以写成两点式或斜截式或点斜式 C可以写成点斜式或截距式 D.可以写成两点式或截距式或斜截式或点斜式 答案B 解析由于直线不与坐标轴平行或重合,所以直线的斜率存在,且直线上任意两点的横坐标及纵坐标都 不相同,所以直线能写成两点式或斜截式或点斜式由于直线在坐标轴上的截距有可能为0,所以直线 不一定能写成截距式.故选B 1
1 2.2.2 直线的两点式方程 课后· 基础巩固 1.经过两点(5,0),(2,-5)的直线方程为( ) A.5x+3y-25=0 B.5x-3y-25=0 C.3x-5y-25=0 D.5x-3y+25=0 答案:B 解析:经过两点(5,0),(2,-5)的直线方程为 𝑦-0 -5-0 = 𝑥-5 2-5 ,整理得 5x-3y-25=0. 故选 B. 2.已知直线 l:ax+y-2=0 在 x 轴和 y 轴上的截距相等,则实数 a 的值是( ) A.1 B.-1 C.-2 或-1 D.-2 或 1 答案:A 解析:显然 a≠0.把直线 l:ax+y-2=0 化为𝑥 2 𝑎 + 𝑦 2 =1. 因为直线 l:ax+y-2=0 在 x 轴和 y 轴上的截距相等, 所以2 𝑎 =2,解得 a=1,故选 A. 3.若一条直线不与坐标轴平行或重合,则它的方程( ) A.可以写成两点式或截距式 B.可以写成两点式或斜截式或点斜式 C.可以写成点斜式或截距式 D.可以写成两点式或截距式或斜截式或点斜式 答案:B 解析:由于直线不与坐标轴平行或重合,所以直线的斜率存在,且直线上任意两点的横坐标及纵坐标都 不相同,所以直线能写成两点式或斜截式或点斜式.由于直线在坐标轴上的截距有可能为 0,所以直线 不一定能写成截距式.故选 B
志鸿优化系列丛书 志鸿优化网,永远提供更新的: 丛书主编任志湖。 http://www.zhyh.org 4直线总-方在y轴上的截距是( ) A.lbl B.-b2 C.b2 D.±b 含案B 解析令x=0,得y=- 5.(多选题)若直线1的横截距与纵截距都是负数,则下列说法错误的是() A.I的倾斜角为锐角且不过第二象限 B.1的倾斜角为钝角且不过第一象限 C.I的倾斜角为锐角且不过第四象限 D.I的倾斜角为钝角且不过第三象限 客案ACD 解析依题意知,直线1的截距式方程为盖+名-1(>0,b>0),显然直线1过第二、三、四象限,而不会过 第一象限,且倾斜角为钝角,故选ACD 6直线4-名1和直线h若-兰1在同一平面直角坐标系中的位置可以是() 含案A 解析将两条直线方程化为藏距式方程分别为后+名-l管+名=1,根据山的位置判断α6b的正负,再嗡定 2的位置,知A符合 7.己知直线I过点P(-1,2),分别与x轴、y轴交于点A,B,若P为线段AB的中点,则直线1的方程 为一 B P. 32 2
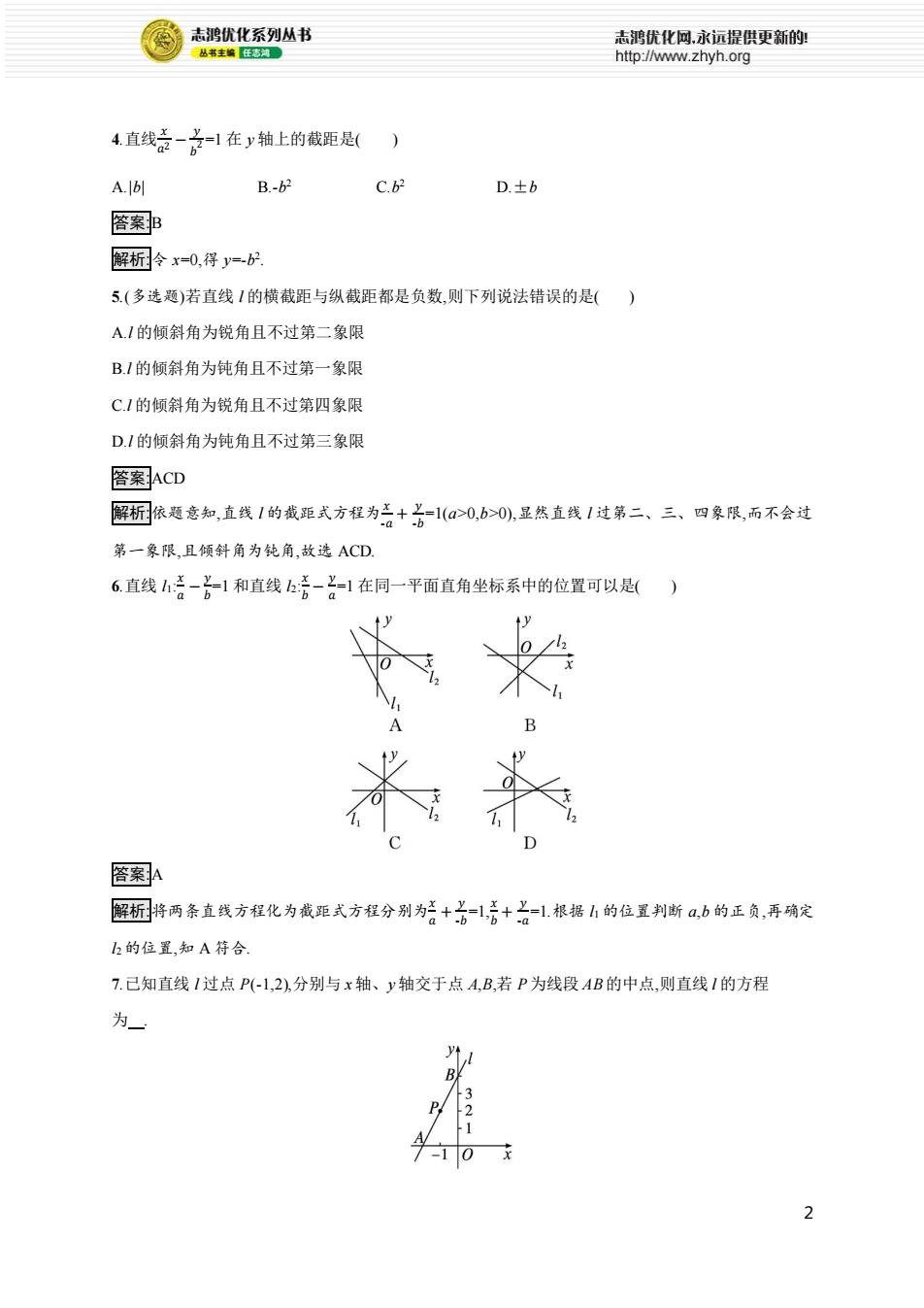
2 4.直线 𝑥 𝑎2 − 𝑦 𝑏 2=1 在 y 轴上的截距是( ) A.|b| B.-b 2 C.b 2 D.±b 答案:B 解析:令 x=0,得 y=-b 2 . 5.(多选题)若直线 l 的横截距与纵截距都是负数,则下列说法错误的是( ) A.l 的倾斜角为锐角且不过第二象限 B.l 的倾斜角为钝角且不过第一象限 C.l 的倾斜角为锐角且不过第四象限 D.l 的倾斜角为钝角且不过第三象限 答案:ACD 解析:依题意知,直线 l 的截距式方程为𝑥 -𝑎 + 𝑦 -𝑏 =1(a>0,b>0),显然直线 l 过第二、三、四象限,而不会过 第一象限,且倾斜角为钝角,故选 ACD. 6.直线 l1: 𝑥 𝑎 − 𝑦 𝑏 =1 和直线 l2: 𝑥 𝑏 − 𝑦 𝑎 =1 在同一平面直角坐标系中的位置可以是( ) 答案:A 解析:将两条直线方程化为截距式方程分别为𝑥 𝑎 + 𝑦 -𝑏 =1,𝑥 𝑏 + 𝑦 -𝑎 =1.根据 l1 的位置判断 a,b 的正负,再确定 l2 的位置,知 A 符合. 7.已知直线 l 过点 P(-1,2),分别与 x 轴、y 轴交于点 A,B,若 P 为线段 AB 的中点,则直线 l 的方程 为

志鸿优化系列丛书 志鸿优化网,永远提供更新的! 丛书主编任志湖。 http://www.zhyh.org 含案2xy+4=0 解析设Ax,0),B(0,以.由P←1,2)为AB的中点,得 (x+01, 2 0+y=2 得子 . 由藏距式得直线1的方程为支+-1, 即2x-y+4=0. 8.过点(1,3)且在x轴上的截距为2的直线方程是 客案3x+y6=0 解析由题意知直线过点(2,0), 又直钱过点(1,3)由两点式可得器=器 整理得3x+y-6=0, 9.过点(0,3),且在两坐标轴上截距之和等于5的直线方程是 靥案蛋+1 解析设直线方程为:+治1, 8+名-5解得023 则直线方程为+学1 10.求经过点A(-2,3),B4,-1)的直线的两点式方程,并把它化成点斜式、斜截式和截距式 图过A,B两点的直线的两点式方程是器-号 因为k4B= 号-号所以点斜式方程为1一号4 4(-2) 斜戴式方程为=子月 成矩或方和动十雪 11.三角形的顶点坐标为A(0,-5),B(-3,3),C(2,0),求直线AB和直线AC的方程 解直线AB过A0,-5),B(3,3)两点, 由两点式方程,得=品 整理得直线AB的方程为8r+3y+15=0. 又直线AC过A(0,-5),C(2,0)两点, 3
3 答案:2x-y+4=0 解析:设 A(x,0),B(0,y).由 P(-1,2)为 AB 的中点,得{ 𝑥+0 2 = -1, 0+𝑦 2 = 2, 解得{ 𝑥 = -2, 𝑦 = 4. 由截距式得直线 l 的方程为𝑥 -2 + 𝑦 4 =1, 即 2x-y+4=0. 8.过点(1,3)且在 x 轴上的截距为 2 的直线方程是 . 答案:3x+y-6=0 解析:由题意知直线过点(2,0), 又直线过点(1,3),由两点式,可得𝑦-0 3-0 = 𝑥-2 1-2 , 整理得 3x+y-6=0. 9.过点(0,3),且在两坐标轴上截距之和等于 5 的直线方程是 . 答案: 𝑥 2 + 𝑦 3 =1 解析:设直线方程为𝑥 𝑎 + 𝑦 𝑏 =1, 则{ 𝑏 = 3, 𝑎 + 𝑏 = 5, 解得 a=2,b=3. 则直线方程为𝑥 2 + 𝑦 3 =1. 10.求经过点 A(-2,3),B(4,-1)的直线的两点式方程,并把它化成点斜式、斜截式和截距式. 解:过 A,B 两点的直线的两点式方程是𝑦-3 -1-3 = 𝑥-(-2) 4-(-2) . 因为 kAB= -1-3 4-(-2) =- 2 3 ,所以点斜式方程为 y+1=- 2 3 (x-4). 斜截式方程为 y=- 2 3 x+5 3 . 截距式方程为𝑥 5 2 + 𝑦 5 3 =1. 11.三角形的顶点坐标为 A(0,-5),B(-3,3),C(2,0),求直线 AB 和直线 AC 的方程. 解:直线 AB 过 A(0,-5),B(-3,3)两点, 由两点式方程,得 𝑦+5 3+5 = 𝑥-0 -3-0 . 整理得直线 AB 的方程为 8x+3y+15=0. 又直线 AC 过 A(0,-5),C(2,0)两点

志鸿优化系列丛书 志鸿优化网永远提供更新的! 丛书主编任志湖。 http://www.zhyh.org 由藏距式得+÷1 整理得直线AC的方程为5x-2y10=0. 拓展提高 1.己知直线ar+by+c=0如图所示,则( A.若c>0,则a>0,b>0 B.若c>0,则a0 C.若c0,b0,b>0 答案p 解标由a++c-0,得斜率一会直线在x轴、y轴上的藏距分别为台云 如题图,k0. 80,-80,…ac0,b>0:若c>0,则a<0,b<0. 2.已知A(3,0),B(0,4),直线AB上一动点Px,y),则xy的最大值是 含案 解标直线AB的方程为+¥-1, 设P(x,则x=3, 故y=32-y2+4圳-022+4]≤3 即当P点坐标为(侵2)时,y取得最大值3。 3.过点P(3,2),且在两坐标轴上的截距相等的直线的方程是 答案卫x-3y-0或x+5=-0 解0当直线过原点时,斜率等于织=号故直线的方程为)学即2x-3)-0, ②当直线不过原点时,设直线的方程为x+y+m=0,把P(3,2)的坐标代入直线的方程得m=-5,故直线方 程为x+5=0. 4
4 由截距式得𝑥 2 + 𝑦 -5 =1, 整理得直线 AC 的方程为 5x-2y-10=0. 拓展提高 1.已知直线 ax+by+c=0 如图所示,则( ) A.若 c>0,则 a>0,b>0 B.若 c>0,则 a0 C.若 c0,b0,b>0 答案:D 解析:由 ax+by+c=0,得斜率 k=- 𝑎 𝑏 ,直线在 x 轴、y 轴上的截距分别为- 𝑐 𝑎 ,- 𝑐 𝑏 . 如题图,k0. ∵- 𝑐 𝑎 >0,- 𝑐 𝑏 >0,∴ac0,b>0;若 c>0,则 a<0,b<0. 2.已知 A(3,0),B(0,4),直线 AB 上一动点 P(x,y),则 xy 的最大值是 . 答案:3 解析:直线 AB 的方程为𝑥 3 + 𝑦 4 =1, 设 P(x,y),则 x=3- 3 4 y, 故 xy=3y- 3 4 y 2= 3 4 (-y 2+4y)= 3 4 [-(y-2)2+4]≤3, 即当 P 点坐标为( 3 2 ,2)时,xy 取得最大值 3. 3.过点 P(3,2),且在两坐标轴上的截距相等的直线的方程是 . 答案:2x-3y=0 或 x+y-5=0 解析:①当直线过原点时,斜率等于2-0 3-0 = 2 3 ,故直线的方程为 y= 2 3 x,即 2x-3y=0. ②当直线不过原点时,设直线的方程为 x+y+m=0,把 P(3,2)的坐标代入直线的方程得 m=-5,故直线方 程为 x+y-5=0

志鸿优化系列丛书 志鸿优化网永远提供更新的! 丛书主编任志河。 http://www.zhyh.org 综上所述,满足条件的直线方程为2x-3y-0或x+y-5=0. 4.垂直于直线3x-4-7=0,且与两坐标轴围成的三角形的面积为6的直线在x轴上的截距 是 含案}或3 解析段直钱方程是4红+3少+d=0,分别令)0和x0,得直钱在x轴、y轴上的藏距分别是号号故 6生×引×引=乐解得d-士12,则直线在x轴上的藏距为3或-3. 5.已知直线1经过点P(4,1) (1)若直线1经过点Q(-1,6),求直线1的两点式方程; (2)若直线I在y轴上的截距是在x轴上的截距的2倍,求直线1的方程. 解)已知直线1经过点P4,1Q-1,6,由两点式,得直线1的方程为器=器 (2)由题意知,直线I的斜率存在且不为0,所以设直线1的斜率为k则其方程为上1=Mx-4). 令x0,得y=l4k令y0,得x=4是 由题意得14k-2(4) 解得k或=2. 因此,直线1的方程为1=x4)或1=-2(x4),即x4y=0或2x+y9=0, 6.直线1过点(-3,4),且在两坐标轴上的截距之和为12,求直线1的方程 解段直线1的方程为后+片=1, 则a+b=12.① 又直线1过点(-3,4), 即2+1.② 由0e解得6-8支g=i6 故所求的直线方程为后+]或导+六L, 即x+3y-9=0或4x-y+16=0. 挑战创新 5
5 综上所述,满足条件的直线方程为 2x-3y=0 或 x+y-5=0. 4.垂直于直线 3x-4y-7=0,且与两坐标轴围成的三角形的面积为 6 的直线在 x 轴上的截距 是 . 答案:3 或-3 解析:设直线方程是 4x+3y+d=0,分别令 y=0 和 x=0,得直线在 x 轴、y 轴上的截距分别是- 𝑑 4 ,- 𝑑 3 ,故 6= 1 2 × |- 𝑑 3 | × |- 𝑑 4 | = 𝑑 2 24,解得 d=±12,则直线在 x 轴上的截距为 3 或-3. 5.已知直线 l 经过点 P(4,1), (1)若直线 l 经过点 Q(-1,6),求直线 l的两点式方程; (2)若直线 l 在 y 轴上的截距是在 x 轴上的截距的 2 倍,求直线 l 的方程. 解:(1)已知直线 l 经过点 P(4,1),Q(-1,6),由两点式,得直线 l 的方程为𝑦-1 6-1 = 𝑥-4 -1-4 . (2)由题意知,直线 l 的斜率存在且不为 0,所以设直线 l的斜率为 k,则其方程为 y-1=k(x-4). 令 x=0,得 y=1-4k;令 y=0,得 x=4- 1 𝑘 . 由题意得 1-4k=2(4- 1 𝑘 ), 解得 k=1 4或 k=-2. 因此,直线 l 的方程为 y-1= 1 4 (x-4)或 y-1=-2(x-4),即 x-4y=0 或 2x+y-9=0. 6.直线 l 过点(-3,4),且在两坐标轴上的截距之和为 12,求直线 l 的方程. 解:设直线 l 的方程为𝑥 𝑎 + 𝑦 𝑏 =1, 则 a+b=12.① 又直线 l 过点(-3,4), 即 -3 𝑎 + 4 𝑏 =1.② 由①②解得{ 𝑎 = 9, 𝑏 = 3 或{ 𝑎 = -4, 𝑏 = 16. 故所求的直线方程为𝑥 9 + 𝑦 3 =1 或 𝑥 -4 + 𝑦 16=1, 即 x+3y-9=0 或 4x-y+16=0. 挑战创新

志鸿优化系列丛书 志鸿优化网,永远提供更新的: 丛书主编任志湖。 http://www.zhyh.org 在△ABC中,己知A(5,-2),B(7,3),且AC边的中点M在y轴上,BC边的中点N在x轴上,求: (1)顶点C的坐标 (2)直线MN的方程 解1)设C0,), 则4C边的中点为M(士5,) BC边的中点为N() 因为点M在y轴上, 所以0+5=0, 2 解得0=-5. 又因为点N在x轴上, 所以20 解得功=3. 所以顶点C的坐标为(-5,-3) (2)()可得M(0,-》,1,0), 故由我距式得直线的方程为片+等, 即5x-2y5-0. 6
6 在△ABC 中,已知 A(5,-2),B(7,3),且 AC 边的中点 M 在 y 轴上,BC 边的中点 N 在 x 轴上,求: (1)顶点 C 的坐标; (2)直线 MN 的方程. 解:(1)设 C(x0,y0), 则 AC 边的中点为 M( 𝑥0+5 2 , 𝑦 0 -2 2 ), BC 边的中点为 N( 𝑥0+7 2 , 𝑦 0 +3 2 ). 因为点 M 在 y 轴上, 所以𝑥0+5 2 =0, 解得 x0=-5. 又因为点 N 在 x 轴上, 所以𝑦 0 +3 2 =0, 解得 y0=-3. 所以顶点 C 的坐标为(-5,-3). (2)由(1)可得 M(0,- 5 2 ),N(1,0), 故由截距式得直线 MN 的方程为𝑥 1 + 𝑦 - 5 2 =1, 即 5x-2y-5=0