
4.3.2 独立性检验 1.为了研究高中学生对戏曲的态度(喜欢和不喜欢两种态度)与性别的关系,运用2×2列联表 进行独立性检验,经计算得2-7.01,则认为是否喜欢戏曲与性别有关系的把握为() A.0.1% B.1% C.99% D.99.9% 答案☐c 解析☐由于2-7.01>6.635,因此有99%的把握认为是否喜欢戏曲与性别有关系。 2.利用独立性检验对两个事件A,B是否有关系进行研究,若有99.5%的把握认为事件A和B 有关系则( ) AX2≥6.635 B.23.841,所以有95%的把握认为文化程度与月收入有关系。 4.通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表 性别 是否爱好某项运动 男 总计 女 爱好 40 20 50 不爱好 20 B0 8 总计 50 50 110 计算X2 110x40x30-20x207.8 60×50×60×50 则下列结论正确的是( A.有99%的把握认为爱好该项运动与性别有关 B.有99%的把握认为爱好该项运动与性别无关 C.在犯错误的概率不超过0.1%的前提下,认为爱好该项运动与性别有关 D.在犯错误的概率不超过0.1%的前提下,认为爱好该项运动与性别无关 含案]A
4.3.2 独立性检验 1.为了研究高中学生对戏曲的态度(喜欢和不喜欢两种态度)与性别的关系,运用 2×2 列联表 进行独立性检验,经计算得 χ 2=7.01,则认为是否喜欢戏曲与性别有关系的把握为( ) A.0.1% B.1% C.99% D.99.9% 答案 C 解析 由于 χ 2=7.01>6.635,因此有 99%的把握认为是否喜欢戏曲与性别有关系. 2.利用独立性检验对两个事件 A,B 是否有关系进行研究,若有 99.5%的把握认为事件 A 和 B 有关系,则( ) A.χ 2≥6.635 B.χ 23.841,所以有 95%的把握认为文化程度与月收入有关系. 4.通过随机询问 110 名性别不同的大学生是否爱好某项运动,得到如下的列联表. 是否爱好某项运动 性别 总计 男 女 爱好 40 20 60 不爱好 20 30 50 总计 60 50 110 计算 χ 2= 110×(40×30-20×20) 2 60×50×60×50 ≈7.8. 则下列结论正确的是( ) A.有 99%的把握认为爱好该项运动与性别有关 B.有 99%的把握认为爱好该项运动与性别无关 C.在犯错误的概率不超过 0.1%的前提下,认为爱好该项运动与性别有关 D.在犯错误的概率不超过 0.1%的前提下,认为爱好该项运动与性别无关 答案 A

解析由27.8及P(2≥6.635)=0.01可知,在犯错误的概率不超过1%的前提下,可认为爱好 该项运动与性别有关,即有99%的把握认为爱好该项运动与性别有关」 5.某电视台在一次对收看文艺节目和新闻节目的观众的抽样调查中,随机抽取了100名电视 观众,相关的数据如下表所示 节目 年龄 文艺节目 新闻节目 总计 20岁至40岁 40 18 58 大于40岁 5 27 42 总计 55 45 100 则有 的把握认为收看新闻节目与观众的年龄有关, 答案 99.9% 解析☐由题意可知 X1002x1510.82,查表可知P210.828=0.01 58×42×55×45 因为10.882>10.828,所以有99.9%的把握认为收看新闻节目与观众的年龄有关 6.某大学统计初步”课程的教师随机调查了选该课的一些学生的情况,具体数据如下表」 别 非统计专业 统计专业 13 10 女 20 为了判断主修统计专业是否与性别有关系,根据表中的数据,得到?50×x20x ≈4.844 23×27×20×30 因为?>3.841,所以判定主修统计专业与性别有关系,这种判断出错的可能性为 答案5% 解析☐因为2>3.841,所以有95%的把握认为主修统计专业与性别有关,出错的可能性为5% 7.用两种检验方法对某食品作沙门氏菌检验,结果如下表: 检验结果 检验方法 总计 阳性 阴性 荧光抗体法 160 5 165 常规培养法 卫6 48 74 总计 186 53 239 能否在犯错误的概率不超过0.1%的前提下,认为采用荧光抗体法与检验结果呈阳性有关系? 解☐由题意可知,2-239×160×485x26足 113.1846.查表可知 165×74×186×53 P2≥10.828)=0.001.因为113.1846>10.828 所以在犯错误的概率不超过0.1%的前提下,可认为采用荧光抗体法与检验结果呈阳性有关 象 8.随着工业化以及城市车辆的增加,城市空气质量指数API一直居高不下,对人体的呼吸系统 造成了影响.现调查了某市500名居民的工作场所和呼吸系统健康情况,得到2×2列联表如下 表所示 是否有呼吸 工作场所 总 系统疾病 室外工作 室内工作 计 有呼吸系统疾病 150 无呼吸系统疾病 100 总计 200
解析 由 χ 2≈7.8 及 P(χ 2≥6.635)=0.01 可知,在犯错误的概率不超过 1%的前提下,可认为爱好 该项运动与性别有关,即有 99%的把握认为爱好该项运动与性别有关. 5.某电视台在一次对收看文艺节目和新闻节目的观众的抽样调查中,随机抽取了 100 名电视 观众,相关的数据如下表所示. 年龄 节目 总计 文艺节目 新闻节目 20 岁至 40 岁 40 18 58 大于 40 岁 15 27 42 总计 55 45 100 则有 的把握认为收看新闻节目与观众的年龄有关. 答案 99.9% 解析 由题意可知, χ 2= 100×(40×27-18×15) 2 58×42×55×45 ≈10.882,查表可知 P(χ 2≥10.828)=0.001. 因为 10.882>10.828,所以有 99.9%的把握认为收看新闻节目与观众的年龄有关. 6.某大学“统计初步”课程的教师随机调查了选该课的一些学生的情况,具体数据如下表. 性别 非统计专业 统计专业 男 13 10 女 7 20 为了判断主修统计专业是否与性别有关系,根据表中的数据,得到 χ 2= 50×(13×20-10×7) 2 23×27×20×30 ≈4.844. 因为 χ 2>3.841,所以判定主修统计专业与性别有关系,这种判断出错的可能性为 . 答案 5% 解析 因为 χ 2>3.841,所以有 95%的把握认为主修统计专业与性别有关,出错的可能性为 5%. 7.用两种检验方法对某食品作沙门氏菌检验,结果如下表: 检验方法 检验结果 总计 阳性 阴性 荧光抗体法 160 5 165 常规培养法 26 48 74 总计 186 53 239 能否在犯错误的概率不超过 0.1%的前提下,认为采用荧光抗体法与检验结果呈阳性有关系? 解 由题意可知,χ 2= 239×(160×48-5×26) 2 165 ×74×186×53 ≈113.184 6.查表可知, P(χ 2≥10.828)=0.001.因为 113.184 6>10.828, 所以在犯错误的概率不超过 0.1%的前提下,可认为采用荧光抗体法与检验结果呈阳性有关 系. 8.随着工业化以及城市车辆的增加,城市空气质量指数 API 一直居高不下,对人体的呼吸系统 造成了影响.现调查了某市 500 名居民的工作场所和呼吸系统健康情况,得到 2×2 列联表如下 表所示. 是否有呼吸 系统疾病 工作场所 总 室外工作 室内工作 计 有呼吸系统疾病 150 无呼吸系统疾病 100 总计 200
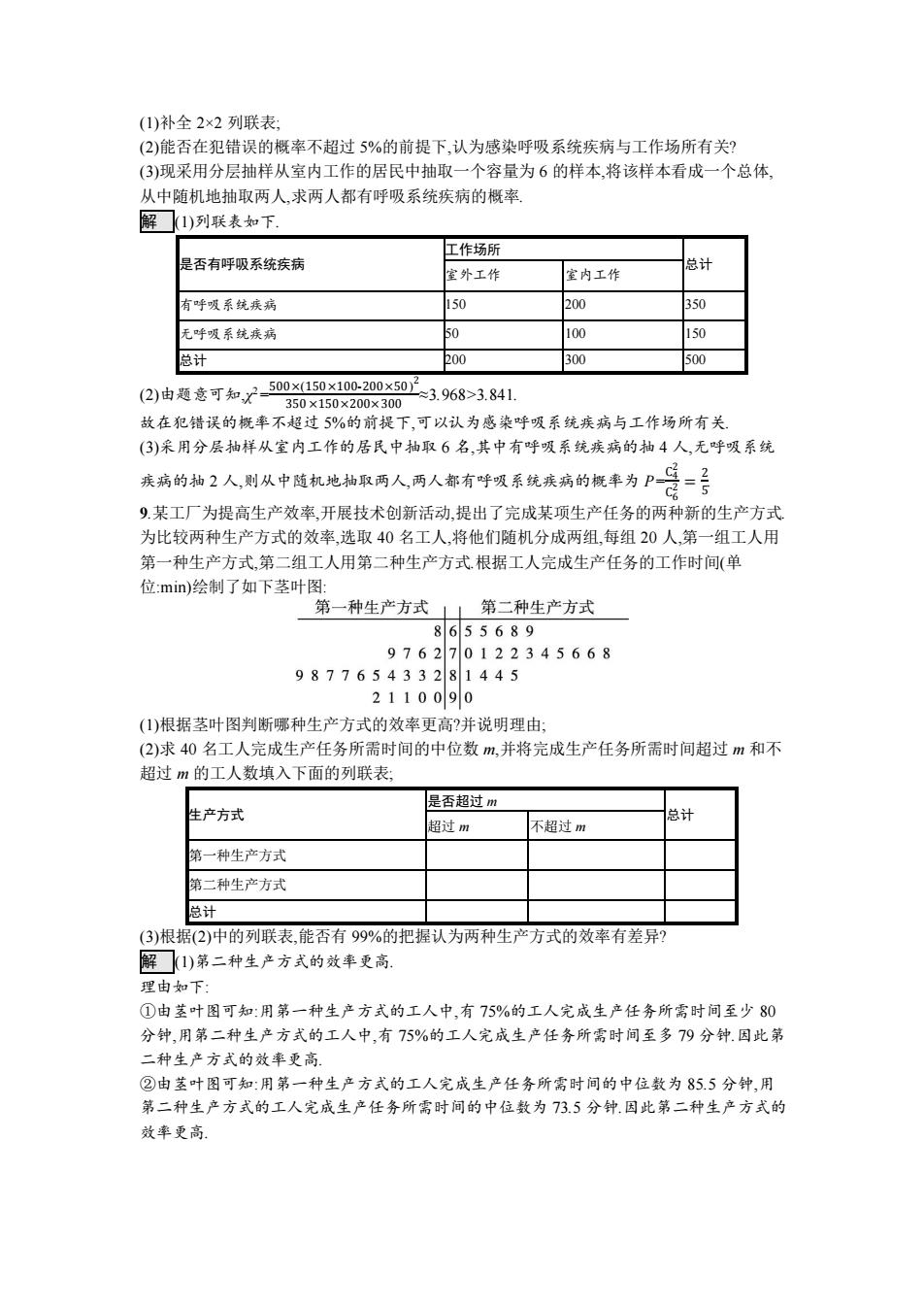
(1)补全2×2列联表: (2)能否在犯错误的概率不超过5%的前提下,认为感染呼吸系统疾病与工作场所有关? (3)现采用分层抽样从室内工作的居民中抽取一个容量为6的样本,将该样本看成一个总体」 从中随机地抽取两人,求两人都有呼吸系统疾病的概率 解【1)列联表如下】 工作场所 是否有呼吸系统疾病 室外工作 室内工作 总计 有呼吸系统疾病 150 200 350 无呼吸系统疾病 0 100 150 总计 P00 300 500 (2)由题意可知,7500x150x100.200x50 350×150×200×300 ≈3.968>3.841 故在犯错误的概率不超过5%的前提下,可以认为感染呼吸系统疾病与工作场所有关」 (3)采用分层抽样从室内工作的居民中抽取6名,其中有呼吸系统疾病的抽4人,无呼吸系统 疾病的抽2人,则从中随机地抽取两人两人都有呼吸系统疾病的概率为P= 9.某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式 为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用 第一种生产方式,第二组工人用第二种生产方式根据工人完成生产任务的工作时间(单 位min)绘制了如下茎叶图: 第一种生产方式」L第二种生产方式 8655689 976270122345668 987765433281445 2110090 (1)根据茎叶图判断哪种生产方式的效率更高?并说明理由: (2)求40名工人完成生产任务所需时间的中位数m,并将完成生产任务所需时间超过m和不 超过m的工人数填入下面的列联表: 是否超过m 生产方式 总计 超过m 不超过m 第一种生产方式 第二种生产方式 总计 (3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异? 解☐)第二种生产方式的效率更高. 理由如下: ①由茎叶图可知:用第一种生产方式的工人中,有75%的工人完成生产任务所需时间至少80 分钟,用第二种生产方式的工人中,有75%的工人完成生产任务所需时间至多79分钟.因此第 二种生产方式的效率更高 ②由茎叶图可知:用第一种生产方式的工人完成生产任务所需时间的中位数为85.5分钟,用 第二种生产方式的工人完成生产任务所需时间的中位数为73.5分钟.因此第二种生产方式的 效率更高
(1)补全 2×2 列联表; (2)能否在犯错误的概率不超过 5%的前提下,认为感染呼吸系统疾病与工作场所有关? (3)现采用分层抽样从室内工作的居民中抽取一个容量为 6 的样本,将该样本看成一个总体, 从中随机地抽取两人,求两人都有呼吸系统疾病的概率. 解 (1)列联表如下. 是否有呼吸系统疾病 工作场所 总计 室外工作 室内工作 有呼吸系统疾病 150 200 350 无呼吸系统疾病 50 100 150 总计 200 300 500 (2)由题意可知,χ 2= 500×(150×100-200×50) 2 350 ×150×200×300 ≈3.968>3.841. 故在犯错误的概率不超过 5%的前提下,可以认为感染呼吸系统疾病与工作场所有关. (3)采用分层抽样从室内工作的居民中抽取 6 名,其中有呼吸系统疾病的抽 4 人,无呼吸系统 疾病的抽 2 人,则从中随机地抽取两人,两人都有呼吸系统疾病的概率为 P=C4 2 C6 2 = 2 5 . 9.某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式. 为比较两种生产方式的效率,选取 40 名工人,将他们随机分成两组,每组 20 人,第一组工人用 第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单 位:min)绘制了如下茎叶图: (1)根据茎叶图判断哪种生产方式的效率更高?并说明理由; (2)求 40 名工人完成生产任务所需时间的中位数 m,并将完成生产任务所需时间超过 m 和不 超过 m 的工人数填入下面的列联表; 生产方式 是否超过 m 总计 超过 m 不超过 m 第一种生产方式 第二种生产方式 总计 (3)根据(2)中的列联表,能否有 99%的把握认为两种生产方式的效率有差异? 解 (1)第二种生产方式的效率更高. 理由如下: ①由茎叶图可知:用第一种生产方式的工人中,有 75%的工人完成生产任务所需时间至少 80 分钟,用第二种生产方式的工人中,有 75%的工人完成生产任务所需时间至多 79 分钟.因此第 二种生产方式的效率更高. ②由茎叶图可知:用第一种生产方式的工人完成生产任务所需时间的中位数为 85.5 分钟,用 第二种生产方式的工人完成生产任务所需时间的中位数为 73.5 分钟.因此第二种生产方式的 效率更高

③由茎叶图可知:用第一种生产方式的工人完成生产任务平均所需时间高于80分钟;用第二 种生产方式的工人完成生产任务平均所需时间低于80分钟.因此第二种生产方式的效率更 高. ④由茎叶图可知:用第一种生产方式的工人完成生产任务所需时间分布在茎8上的最多,关于 茎8大致呈对称分布,用第二种生产方式的工人完成生产任务所需时间分布在茎7上的最多, 关于茎7大致呈对称分布.又用两种生产方式的工人完成生产任务所需时间分布的区间相同, 故可以认为用第二种生产方式完成生产任务所需的时间比用第一种生产方式完成生产任务 所需的时间更少因此第二种生产方式的效率更高 (以上给出了4种理由,写出其中任意一种或其他合理理由均可) (2)由茎叶图知m7981-80 2 列联表如下: 是否超过m 生产方式 总计 超过m 不超过m 第一种生产方式 15 5 20 第二种生产方式 5 15 o 总计 20 20 40 (3)由题意可知X40X5x155x5 20×20×20×20 -=10>6.635 故有99%的把握认为两种生产方式的效率有差异
③由茎叶图可知:用第一种生产方式的工人完成生产任务平均所需时间高于 80 分钟;用第二 种生产方式的工人完成生产任务平均所需时间低于 80 分钟.因此第二种生产方式的效率更 高. ④由茎叶图可知:用第一种生产方式的工人完成生产任务所需时间分布在茎 8 上的最多,关于 茎 8 大致呈对称分布;用第二种生产方式的工人完成生产任务所需时间分布在茎 7 上的最多, 关于茎 7 大致呈对称分布.又用两种生产方式的工人完成生产任务所需时间分布的区间相同, 故可以认为用第二种生产方式完成生产任务所需的时间比用第一种生产方式完成生产任务 所需的时间更少.因此第二种生产方式的效率更高. (以上给出了 4 种理由,写出其中任意一种或其他合理理由均可) (2)由茎叶图知 m= 79+81 2 =80. 列联表如下: 生产方式 是否超过 m 总计 超过 m 不超过 m 第一种生产方式 15 5 20 第二种生产方式 5 15 20 总计 20 20 40 (3)由题意可知,χ 2= 40×(15×15-5×5) 2 20×20×20×20 =10>6.635, 故有 99%的把握认为两种生产方式的效率有差异