
4.3 统计模型 4.3.1一元线性回归模型 第1课时 相关关系、回归直线方程、回归直 线方程的性质 1.(多选题)四名同学根据各自的样本数据研究变量x,y之间的相关关系,并求得回归直线方程, 分别得到以下四个结论,其中一定不正确的是() Ay与x负相关,且y=2.347x-6.423 By与x负相关,且y=-3.476x+5.648 Cy与x正相关,且y=5.437x+8.493 Dy与x正相关,且y=-4.326x-4.578 答案AD 解析☐当y与x线性相关时y与x正相关的充要条件是b>0y与x负相关的充要条件是 b0,b>0 B.a>0,b0 D.a0,b<0. 4.己知变量x与y正相关,且由观测数据算得元-3,=3.5,则由该观测数据求得的回归直线方 程可能是()
4.3 统计模型 4.3.1 一元线性回归模型 第 1 课时 相关关系、回归直线方程、回归直 线方程的性质 1.(多选题)四名同学根据各自的样本数据研究变量 x,y 之间的相关关系,并求得回归直线方程, 分别得到以下四个结论,其中一定不正确的是( ) A.y 与 x 负相关,且𝑦 ^ =2.347x-6.423 B.y 与 x 负相关,且y ^ =-3.476x+5.648 C.y 与 x 正相关,且𝑦 ^ =5.437x+8.493 D.y 与 x 正相关,且𝑦 ^ =-4.326x-4.578 答案 AD 解析 当 y 与 x 线性相关时,y 与 x 正相关的充要条件是𝑏 ^ >0,y 与 x 负相关的充要条件是 b ^ 0,𝑏 ^ >0 B.𝑎 ^ >0,𝑏 ^ 0 D.𝑎 ^ 0,b ^ <0. 4.已知变量 x 与 y 正相关,且由观测数据算得𝑥=3,𝑦=3.5,则由该观测数据求得的回归直线方 程可能是( )

A.y=0.4x+2.3 B.y=2x-2.4 Cy=-2x+9.5 D.y=-0.3x+4.4 答案A 解析由变量x与y正相关,可知C,D均错.又回归直线经过样本点的中心(3,3.5),经验证,可 知A正确,B错误.故选A 5.过(3,10),(7,20),(11,24)三点的回归直线方程是() Ay=1.75+5.75x B.y=-1.75+5.75x C.y=5.75+1.75x D.y=5.75-1.75x 答案C 解析由题意易得,b=1.75,a=5.75,故所求的回归直线方程为y=5.75+1.75x故选C 6.为了均衡教育资源,加大对偏远地区的教育投入,调查了某地若干户家庭的年收入x(单位:万 元)和年教育支出单位:万元).调查显示,年收入x与年教育支出y具有线性相关关系,并由 调查数据得到y关于x的回归直线方程为y=0.15x+0.2.由回归直线方程可知,家庭年收入每 增加1万元,年教育支出平均增加 万元 答案☐b.15 7.期中考试后,某校高三(9)班对全班65名学生的成绩进行分析,得到数学成绩y关于总成绩x 的回归直线方程为y=6+0.4x由此可以估计,若两名同学的总成绩相差50分,则他们的数学成 绩大约相差 分 答案0 A 解析☐由回归系数b-0.4可知,x每增大1个单位,y增大0.4个单位,故两名同学的总成绩相 差50分,他们的数学成绩大约相差50×0.4=20(分). 8.在一项关于16艘轮船的研究中,船的吨位区间为192,3246(单位:吨),船员的人数为5-32, 船员人数y关于吨位x的回归直线方程为y=9.5+0.0062x, (1)若两艘船的吨位相差1000,估计这两艘船的船员人数相差多少; (2)估计吨位最大的船和最小的船的船员人数, 解☐1)由题意可知,这两艘船的船员人数大约相差0.0062×10006. (2)当x=192时,y=9.5+0.0062×192≈11, 当x=3246时,y=9.5+0.0062×3246≈30. 故估计吨位最大的船和最小的船的船员人数分别为30和11. 9.从某居民区随机抽取10个家庭,获得第i个家庭的月收入x(单位:千元)与月储蓄(单位: 千元的数据资料,算得足,-80,=20,足x0y=184号x好=720, 10 10 10 1 运1 i=1 i=1 (I)求家庭的月储蓄y关于月收入x的回归直线方程y=bx+a; (2)判断变量x与y之间是正相关还是负相关
A.𝑦 ^ =0.4x+2.3 B.𝑦 ^ =2x-2.4 C.𝑦 ^ =-2x+9.5 D.𝑦 ^ =-0.3x+4.4 答案 A 解析 由变量 x 与 y 正相关,可知 C,D 均错.又回归直线经过样本点的中心(3,3.5),经验证,可 知 A 正确,B 错误.故选 A. 5.过(3,10),(7,20),(11,24)三点的回归直线方程是( ) A.𝑦 ^ =1.75+5.75x B.y ^ =-1.75+5.75x C.𝑦 ^ =5.75+1.75x D.𝑦 ^ =5.75-1.75x 答案 C 解析 由题意易得,𝑏 ^ =1.75,a ^ =5.75,故所求的回归直线方程为𝑦 ^ =5.75+1.75x.故选 C. 6.为了均衡教育资源,加大对偏远地区的教育投入,调查了某地若干户家庭的年收入 x(单位:万 元)和年教育支出 y(单位:万元).调查显示,年收入 x 与年教育支出 y 具有线性相关关系,并由 调查数据得到 y 关于 x 的回归直线方程为𝑦 ^ =0.15x+0.2.由回归直线方程可知,家庭年收入每 增加 1 万元,年教育支出平均增加 万元. 答案 0.15 7.期中考试后,某校高三(9)班对全班 65 名学生的成绩进行分析,得到数学成绩 y 关于总成绩 x 的回归直线方程为𝑦 ^ =6+0.4x.由此可以估计,若两名同学的总成绩相差 50 分,则他们的数学成 绩大约相差 分. 答案 20 解析 由回归系数𝑏 ^ =0.4 可知,x 每增大 1 个单位,y ^ 增大 0.4 个单位,故两名同学的总成绩相 差 50 分,他们的数学成绩大约相差 50×0.4=20(分). 8.在一项关于 16 艘轮船的研究中,船的吨位区间为[192,3 246](单位:吨),船员的人数为 5~32, 船员人数 y 关于吨位 x 的回归直线方程为𝑦 ^ =9.5+0.006 2x, (1)若两艘船的吨位相差 1 000,估计这两艘船的船员人数相差多少; (2)估计吨位最大的船和最小的船的船员人数. 解 (1)由题意可知,这两艘船的船员人数大约相差 0.006 2×1 000≈6. (2)当 x=192 时,𝑦 ^ =9.5+0.006 2×192≈11, 当 x=3 246 时,𝑦 ^ =9.5+0.006 2×3 246≈30. 故估计吨位最大的船和最小的船的船员人数分别为 30 和 11. 9.从某居民区随机抽取 10 个家庭,获得第 i 个家庭的月收入 xi(单位:千元)与月储蓄 yi(单位: 千元)的数据资料,算得 ∑ 𝑖=1 10 xi=80, ∑ 𝑖=1 10 yi=20, ∑ 𝑖=1 10 xiyi=184, ∑ 𝑖=1 10 𝑥𝑖 2=720. (1)求家庭的月储蓄 y 关于月收入 x 的回归直线方程𝑦 ^ = 𝑏 ^ x+𝑎 ^ ; (2)判断变量 x 与 y 之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄. 解☐1)由题意知,n=10, 11 元=-8=10台” ∑片=2,则b= 184-10×8×2=0.3,Q=2-0.3×8=-0.4 720-10×82 故所求回归直线方程为y=0.3x-0.4. (2)因为b=0.3>0,所以x与y之间是正相关 (3)当x=7时,y=0.3×7-0.4=1.7. 故该家庭的月储蓄约为1.7千元 10.某同学家开了一个小卖部,他为了研究气温对热饮销售的影响,经过统计,得到卖出的热饮 杯数y与当天气温x(单位:℃)的对比表如下 气温C -5 0 4 12 15 19 2327 31 36 读出的热 156 150 132 128 130 116 104 93 54 饮杯数y (1)作出散点图; (2)y与x是正相关还是负相关: (3)求y关于x的回归直线方程 (4)若某天的气温为2℃,预测这天卖出的热饮杯数. 解1)作出散,点图如图所示 ↑y 160 1504 140 130 120 110 100 90 8 0 60 50A 10 0 20 3040x (2)由散点图可知y与x负相关, (6)根据数据可知,元=曾,7=10,b2352,日=了-b2147767 故所求的回归直线方程为y=-2.352x+147.767 (4)当x=2时,y=143.063.因此,当某天的气温为2℃时,这天大约可以卖出143杯热饮
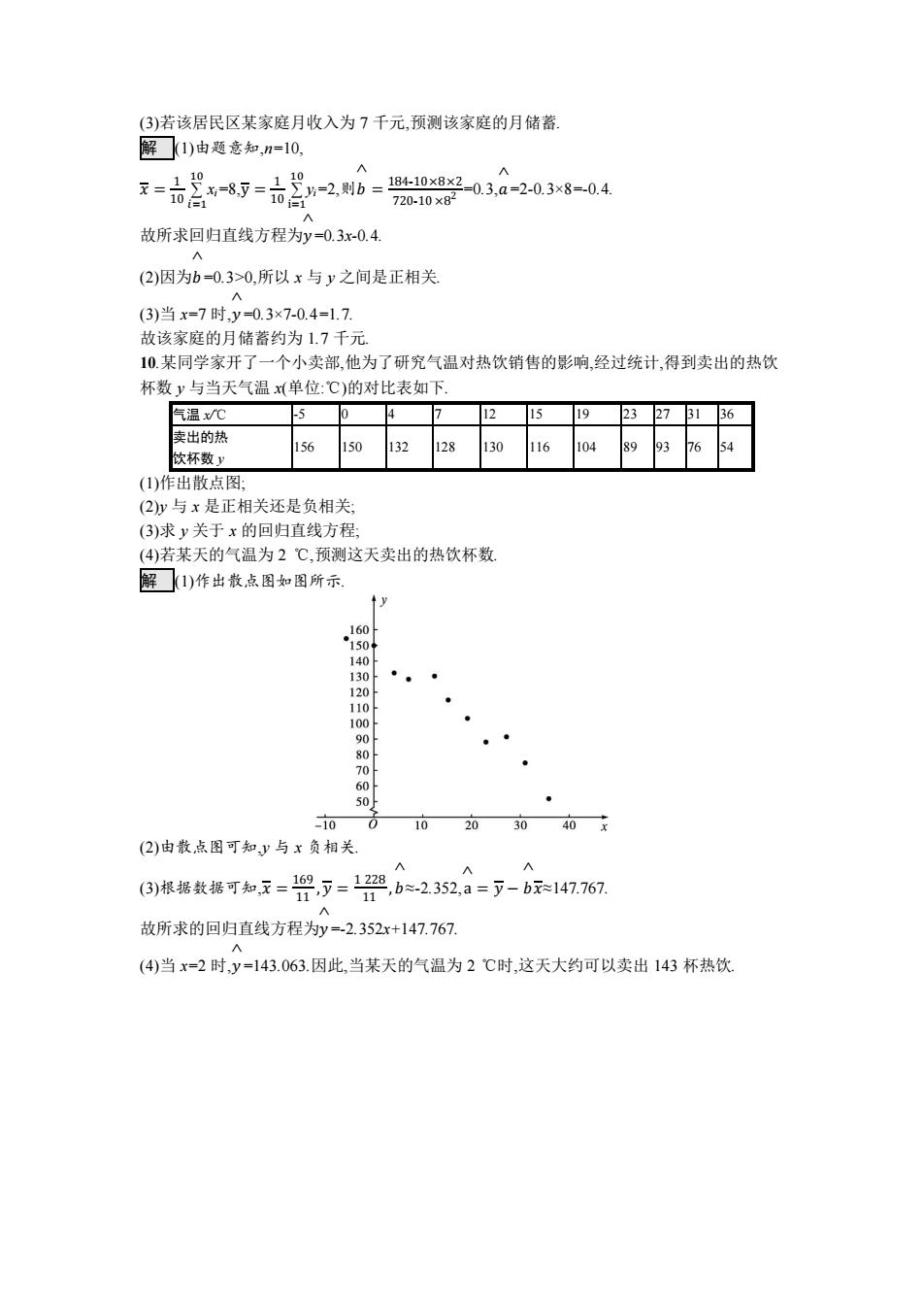
(3)若该居民区某家庭月收入为 7 千元,预测该家庭的月储蓄. 解 (1)由题意知,n=10, 𝑥 = 1 10 ∑ 𝑖=1 10 xi=8,y = 1 10 ∑ i=1 10 yi=2,则𝑏 ^ = 184-10×8×2 720-10 ×8 2 =0.3,𝑎 ^ =2-0.3×8=-0.4. 故所求回归直线方程为𝑦 ^ =0.3x-0.4. (2)因为𝑏 ^ =0.3>0,所以 x 与 y 之间是正相关. (3)当 x=7 时,𝑦 ^ =0.3×7-0.4=1.7. 故该家庭的月储蓄约为 1.7 千元. 10.某同学家开了一个小卖部,他为了研究气温对热饮销售的影响,经过统计,得到卖出的热饮 杯数 y 与当天气温 x(单位:℃)的对比表如下. 气温 x/℃ -5 0 4 7 12 15 19 23 27 31 36 卖出的热 饮杯数 y 156 150 132 128 130 116 104 89 93 76 54 (1)作出散点图; (2)y 与 x 是正相关还是负相关; (3)求 y 关于 x 的回归直线方程; (4)若某天的气温为 2 ℃,预测这天卖出的热饮杯数. 解 (1)作出散点图如图所示. (2)由散点图可知,y 与 x 负相关. (3)根据数据可知,𝑥 = 169 11 , 𝑦 = 1 228 11 , 𝑏 ^ ≈-2.352,a ^ = 𝑦 − 𝑏 ^ 𝑥≈147.767. 故所求的回归直线方程为𝑦 ^ =-2.352x+147.767. (4)当 x=2 时,𝑦 ^ =143.063.因此,当某天的气温为 2 ℃时,这天大约可以卖出 143 杯热饮