第2课时; 相关系数、非线性回归 1.甲、乙、丙、丁四名学生各自对X,Y两个变量的线性相关性进行试验,并用回归分析方法 分别求得相关系数r如下表. 生 甲 丙 0.82 D.78 0.69 0.85 则这四名同学的试验结果能体现出X,Y两个变量有更强的线性相关性的是( A.甲 B.乙 C.丙 D.丁 答案D 2.某商品的销售量(单位:件)与销售价格(单位:元/件)存在线性相关关系根据一组样本数据 (,i=1,2,,n),用最小二乘法建立的回归直线方程为y-5x+150,则下列结论正确的是 () Ay与x正相关 B.若r表示y与x的线性相关系数,则r=-5 C.当销售价格为10元时,销售量为100件 D.当销售价格为10元时,销售量为100件左右 答案D 解析由回归直线方程知y与x负相关,故A错.因为r表示y与x的线性相关系数,所以 ls1,故B错.当x=10时,y=-5×10+150=100,即销售量为100件左右,故C错,D正确.故选D, 3.在一次对人体脂肪含量和年龄关系的研究中,研究人员获得了一组样本数据,并制作成人体 脂肪含量与年龄关系的散点图如图所示根据该图,下列结论正确的是() 脂肪含量/% 35 30 25 204 15 10 0W5202530354045505560年龄 A.人体脂肪含量与年龄的相关系数>0,且脂肪含量的中位数等于20% B.人体脂肪含量与年龄的相关系数r>0,且脂肪含量的中位数小于20% C.人体脂肪含量与年龄的相关系数0.因为中间两个数据的平 均数在15%到20%之间,所以脂肪含量的中位数小于20%. 4.变量X与Y相对应的一组数据为(10,1).11.3,2).(11.8,3),(12.5,4),(13,5);变量U与V相对应 的一组数据为10,5),(11.3,4),(11.8,3).(12.5,2),(13,1).n表示变量Y与X之间的相关系数,n表 示变量V与U之间的相关系数,则() A.n<n<0 B.0<n<n C.n<0<r D.n=n
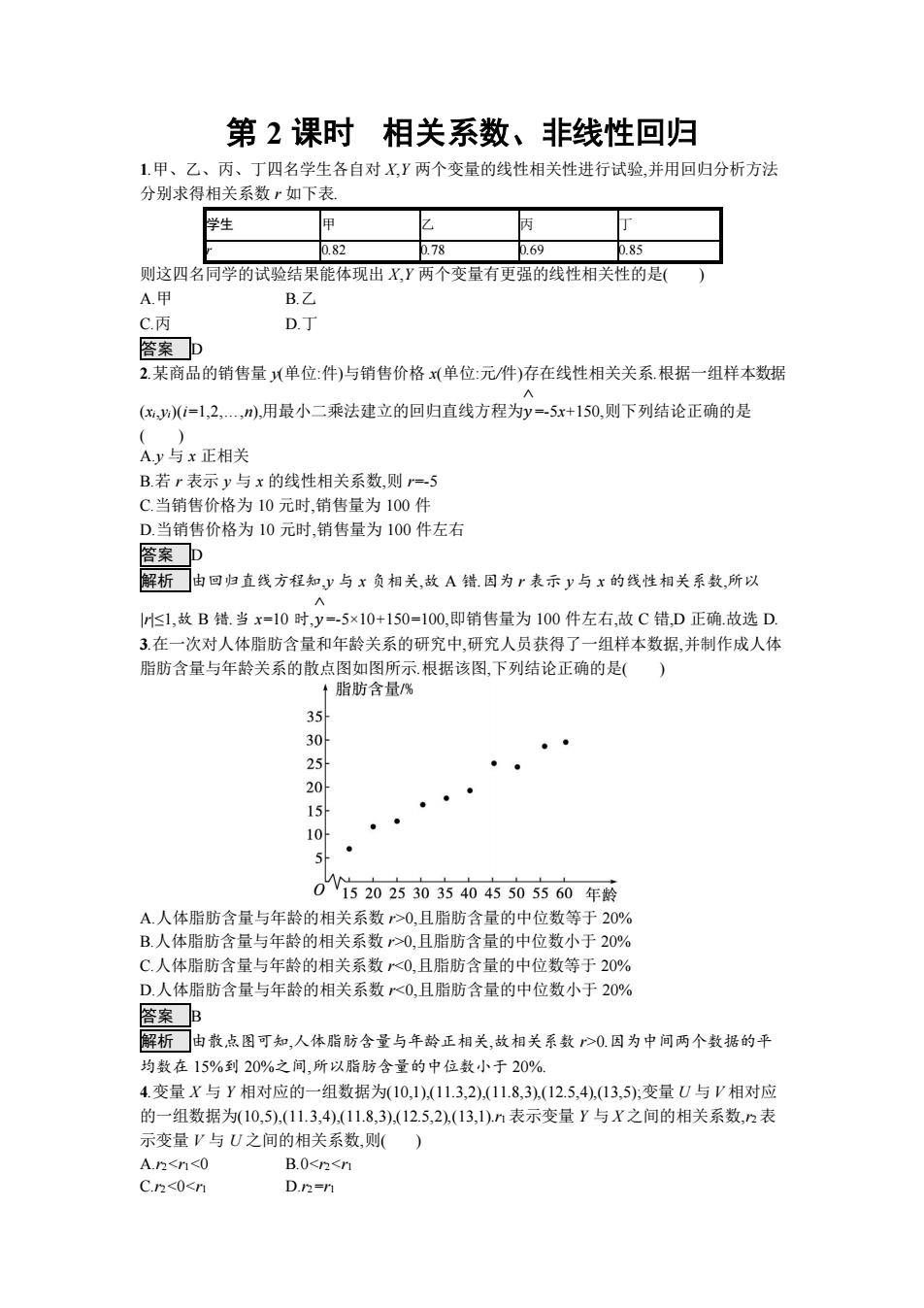
第 2 课时 相关系数、非线性回归 1.甲、乙、丙、丁四名学生各自对 X,Y 两个变量的线性相关性进行试验,并用回归分析方法 分别求得相关系数 r 如下表. 学生 甲 乙 丙 丁 r 0.82 0.78 0.69 0.85 则这四名同学的试验结果能体现出 X,Y 两个变量有更强的线性相关性的是( ) A.甲 B.乙 C.丙 D.丁 答案 D 2.某商品的销售量 y(单位:件)与销售价格 x(单位:元/件)存在线性相关关系.根据一组样本数据 (xi,yi)(i=1,2,…,n),用最小二乘法建立的回归直线方程为𝑦 ^ =-5x+150,则下列结论正确的是 ( ) A.y 与 x 正相关 B.若 r 表示 y 与 x 的线性相关系数,则 r=-5 C.当销售价格为 10 元时,销售量为 100 件 D.当销售价格为 10 元时,销售量为 100 件左右 答案 D 解析 由回归直线方程知,y 与 x 负相关,故 A 错.因为 r 表示 y 与 x 的线性相关系数,所以 |r|≤1,故 B 错.当 x=10 时,𝑦 ^ =-5×10+150=100,即销售量为 100 件左右,故 C 错,D 正确.故选 D. 3.在一次对人体脂肪含量和年龄关系的研究中,研究人员获得了一组样本数据,并制作成人体 脂肪含量与年龄关系的散点图如图所示.根据该图,下列结论正确的是( ) A.人体脂肪含量与年龄的相关系数 r>0,且脂肪含量的中位数等于 20% B.人体脂肪含量与年龄的相关系数 r>0,且脂肪含量的中位数小于 20% C.人体脂肪含量与年龄的相关系数 r0.因为中间两个数据的平 均数在 15%到 20%之间,所以脂肪含量的中位数小于 20%. 4.变量 X 与 Y 相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12.5,4),(13,5);变量 U 与 V 相对应 的一组数据为(10,5),(11.3,4),(11.8,3),(12.5,2),(13,1).r1 表示变量 Y 与 X 之间的相关系数,r2 表 示变量 V 与 U 之间的相关系数,则( ) A.r2<r1<0 B.0<r2<r1 C.r2<0<r1 D.r2=r1
答案☐ 解析由题意可知,Y与X正相关,V与U负相关,故n>0,n<0.故选C 5.对四组数据进行统计,得到的散点图如图所示,则它们的相关系数的大小关系 为 35 30 5 0 5 101520 25 3035 相关系数为r1 图① 25 2 0 1015202530 35 相关系数为r2 图② 5050510 。 5 101520 2530 35 相关系数为r3 图③ 35101570 0 101520253035 相关系数为r4 图④ 答案☐ <r4<片<1 5 6.已知正--20,x子-2-25,2y-2-36,则相关系数r= =1 i=1 i三1 答案☐ 解折裂月 20 7.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据 如下表所示 零件的个数个 2 3 4 6 加工的时间)h p.5 4 4.5 (1)求y与x的相关系数(精确到0.01),并求y关于x的回归直线方程; (2)试预测加工10个零件需要多少时间
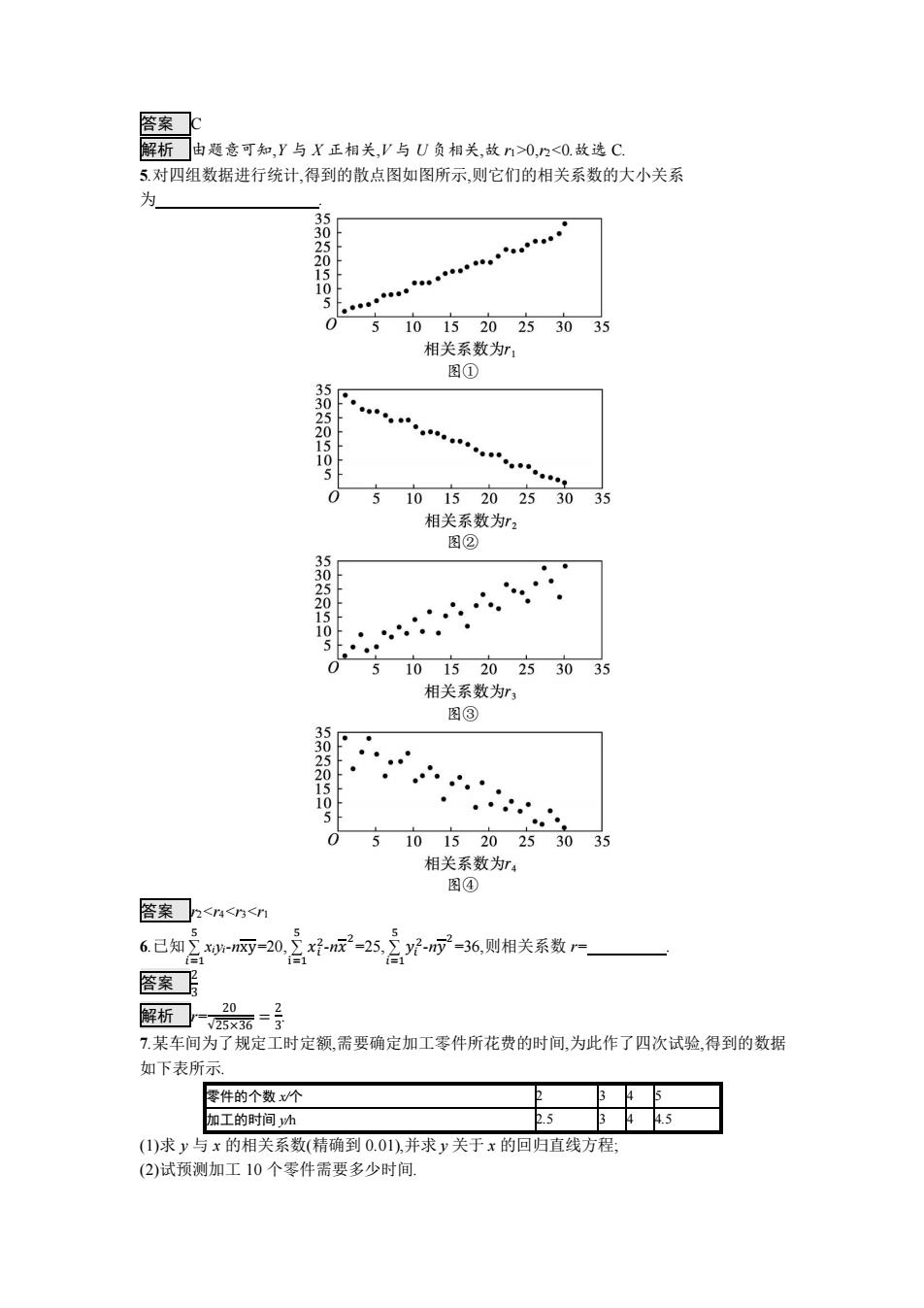
答案 C 解析 由题意可知,Y 与 X 正相关,V 与 U 负相关,故 r1>0,r2<0.故选 C. 5.对四组数据进行统计,得到的散点图如图所示,则它们的相关系数的大小关系 为 . 图① 图② 图③ 图④ 答案 r2<r4<r3<r1 6.已知 ∑ 𝑖=1 5 xiyi-nxy=20, ∑ i=1 5 𝑥𝑖 2 -n𝑥 2 =25, ∑ 𝑖=1 5 𝑦𝑖 2 -n𝑦 2 =36,则相关系数 r= . 答案 2 3 解析 r= 20 √25×36 = 2 3 . 7.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据 如下表所示. 零件的个数 x/个 2 3 4 5 加工的时间 y/h 2.5 3 4 4.5 (1)求 y 与 x 的相关系数(精确到 0.01),并求 y 关于 x 的回归直线方程; (2)试预测加工 10 个零件需要多少时间

爵□1)油表中数据得-355-35含-4含-515套0-52 1 1 则= =0.99, (2x好4x2-4) V=1 i=l 6昌4 =0.7,a=y-bx-1.05 x好4坛 1 故y=0.7x+1.05. (2)当x=10时,y=0.7×10+1.05=8.05, 故预测加工10个零件需要8.05h 8.我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图如图所示. 年生活垃圾无害化处理量y 1.80 1.60 1.40 1.20 1.00 0.80 1 234567— 年份代码t 注:年份代码1~7分别对应年份2008-2014. (1)由折线图看出,可用线性回归模型拟合y与1的关系,请用相关系数加以说明: (2)建立y关于1的回归直线方程(系数精确到0.01),预测2020年我国生活垃圾无害化处理量 附注 7 7 参考数据:∑片=9.32,∑%=40.17, 0-y)2-0.55,V7≈2.646. 1 =1 =1 参考公式:相关系数 是e-0y r示 回归直线方程y=a+b1中斜率和截距的最小二乘估计公式分别为: e-iy-A b= -,a=-b - i=1 解☐)由折线图中的数据和附注中的参考数据得。 i-42.a-tr=28 (y-)2-0.55 年1 1 7 7 w-0-言-t4017-4*932-289 1 i=1 2.89 故产2x2646x0.550.9, 因为y与1的相关系数近似为0.99,说明y与1的线性相关性相当强,所以可以用线性回归模 型拟合y与1的关系 (2)由5=9321.331及0)得, 7
解 (1)由表中数据得,𝑥=3.5,𝑦=3.5, ∑ 𝑖=1 4 xi 2=54, ∑ i=1 4 𝑦𝑖 2=51.5, ∑ 𝑖=1 4 xiyi=52.5, 则 r= ∑ 𝑖=1 4 𝑥𝑖𝑦 𝑖 -4𝑥 𝑦 √( ∑ 𝑖=1 4 𝑥𝑖 2 -4𝑥 2 )( ∑ 𝑖=1 4 𝑦 𝑖 2-4𝑦 2 ) ≈0.99, 𝑏 ^ = ∑ 𝑖=1 4 𝑥𝑖𝑦 𝑖 -4𝑥 𝑦 ∑ 𝑖=1 4 𝑥𝑖 2 -4𝑥 2 =0.7,𝑎 ^ = 𝑦 − 𝑏 ^ 𝑥=1.05, 故𝑦 ^ =0.7x+1.05. (2)当 x=10 时,𝑦 ^ =0.7×10+1.05=8.05, 故预测加工 10 个零件需要 8.05 h. 8.我国 2008 年至 2014 年生活垃圾无害化处理量(单位:亿吨)的折线图如图所示. 注:年份代码 1~7 分别对应年份 2008~2014. (1)由折线图看出,可用线性回归模型拟合 y 与 t 的关系,请用相关系数加以说明; (2)建立 y 关于 t 的回归直线方程(系数精确到 0.01),预测 2020 年我国生活垃圾无害化处理量. 附注: 参考数据: ∑ 𝑖=1 7 yi=9.32, ∑ 𝑖=1 7 tiyi=40.17,√ ∑ 𝑖=1 7 (𝑦𝑖 -𝑦) 2=0.55,√7≈2.646. 参考公式:相关系数 r= ∑ 𝑖=1 𝑛 (𝑡𝑖 -𝑡)(𝑦 𝑖 -𝑦) √ ∑ 𝑖=1 𝑛 (𝑡𝑖 -𝑡) 2 ∑ 𝑖=1 𝑛 (𝑦 𝑖 -𝑦) 2 , 回归直线方程𝑦 ^ = 𝑎 ^ + 𝑏 ^ t 中斜率和截距的最小二乘估计公式分别为: 𝑏 ^ = ∑ 𝑖=1 𝑛 (𝑡𝑖 -𝑡)(𝑦 𝑖 -𝑦) ∑ 𝑖=1 𝑛 (𝑡𝑖 -𝑡) 2 , 𝑎 ^ = 𝑦 − 𝑏 ^ 𝑡. 解 (1)由折线图中的数据和附注中的参考数据得, 𝑡=4, ∑ 𝑖=1 7 (ti-t) 2=28,√ ∑ i=1 7 (𝑦𝑖 -𝑦) 2=0.55, ∑ 𝑖=1 7 (ti-𝑡)(yi-𝑦)= ∑ 𝑖=1 7 tiyi-𝑡 ∑ 𝑖=1 7 yi=40.17-4×9.32=2.89, 故 r≈ 2.89 2×2.646×0.55≈0.99. 因为 y 与 t 的相关系数近似为 0.99,说明 y 与 t 的线性相关性相当强,所以可以用线性回归模 型拟合 y 与 t 的关系. (2)由𝑦 = 9.32 7 ≈1.331 及(1)得

7 (t-0y- b=白1 1_2890.103, (传-2 28 1 a=y-bt1.331-0.103×40.92. 所以y关于1的回归直线方程为y=0.92+0.101. 将2020年对应的1=13代入回归直线方程得y=0.92+0.10×13=2.22 所以预测2020年我国生活垃圾无害化处理量将约为2.22亿吨 9.二手车经销商小王对其所经营的A型号二手汽车的使用年数x与销售价格(单位:万元/ 辆)进行整理,得到如下数据 使用年数x 2 5 销售价格y 12 6.4 4.4 c=Iny 3.00 2.48 .08 1.86 1.48 1.10 z关于x的折线图如图所示 ↑ 2.5 3 1.5 1 0.5 0 34567x ()由折线图可以看出,可以用线性回归模型拟合:与x的关系,请用相关系数加以说明: (2)求y关于x的回归方程,并预测某辆A型号二手汽车使用年数为9年时的销售价格.(回归 直线方程的系数精确到0.01) 参考数据: Σ=187.4,∑=47.64,∑x=139, =1 (x-x)2≈4.18. (z-2)2≈1.53,ln1.48≈0.39 =1 0yr13.96, 1 1 解☐1)由题意,知=2+3+4+56+7)=45, z=名x(3.0+248+208+1.86+1.48+1.10)-2 又是x=47.64, (x-x)2≈4.18, i=1 1 r=153, 1 所以47,646x45Xx2≈.0.9. 4.18×1.53 因为:与x的相关系数大约为-0.99,说明:与x的线性相关性很强,所以可以用线性回归模型 拟合:与x的关系 (2)()可知,b=47.646x45x20.363, 139.6×4.52
𝑏 ^ = ∑ 𝑖=1 7 (𝑡𝑖 -𝑡)(𝑦 𝑖 -𝑦) ∑ 𝑖=1 7 (𝑡𝑖 -𝑡) 2 = 2.89 28 ≈0.103, 𝑎 ^ = 𝑦 − 𝑏 ^ 𝑡≈1.331-0.103×4≈0.92. 所以 y 关于 t 的回归直线方程为𝑦 ^ =0.92+0.10t. 将 2020 年对应的 t=13 代入回归直线方程得𝑦 ^ =0.92+0.10×13=2.22. 所以预测 2020 年我国生活垃圾无害化处理量将约为 2.22 亿吨. 9.二手车经销商小王对其所经营的 A 型号二手汽车的使用年数 x 与销售价格 y(单位:万元/ 辆)进行整理,得到如下数据. 使用年数 x 2 3 4 5 6 7 销售价格 y 20 12 8 6.4 4.4 3 z=ln y 3.00 2.48 2.08 1.86 1.48 1.10 z 关于 x 的折线图如图所示. (1)由折线图可以看出,可以用线性回归模型拟合 z 与 x 的关系,请用相关系数加以说明; (2)求 y 关于 x 的回归方程,并预测某辆 A 型号二手汽车使用年数为 9 年时的销售价格.(回归 直线方程的系数精确到 0.01) 参考数据: ∑ 𝑖=1 6 xiyi=187.4, ∑ i=1 6 xizi=47.64, ∑ 𝑖=1 6 𝑥𝑖 2=139, √ ∑ 𝑖=1 6 (𝑥𝑖 -𝑥) 2 ≈4.18,√ ∑ 𝑖=1 6 (𝑦𝑖 -𝑦) 2 ≈13.96,√ ∑ 𝑖=1 6 (𝑧𝑖 -𝑧) 2 ≈1.53,ln 1.48≈0.39. 解 (1)由题意,知𝑥 = 1 6 ×(2+3+4+5+6+7)=4.5, 𝑧 = 1 6 ×(3.00+2.48+2.08+1.86+1.48+1.10)=2. 又 ∑ 𝑖=1 6 xizi=47.64,√ ∑ i=1 6 (𝑥𝑖 -𝑥) 2 ≈4.18, √ ∑ 𝑖=1 6 (𝑧𝑖 -𝑧) 2 ≈1.53, 所以 r≈ 47.64-6×4.5×2 4.18×1.53 ≈-0.99. 因为 z 与 x 的相关系数大约为-0.99,说明 z 与 x 的线性相关性很强,所以可以用线性回归模型 拟合 z 与 x 的关系. (2)由(1)可知,𝑏 ^ = 47.64-6×4.5×2 139-6×4.5 2 ≈-0.363

a=z-b2+0.363×4.5≈3.63, 故z关于x的回归直线方程为z=0.36x+3.63. 又=lny, 故y关于x的回归方程为y=e036+363 当x=9时,y=e0.36x9+3.63=e0.39 因为ln1.48≈0.39,所以y≈1.48. 故预测某辆A型号二手汽车使用年数为9年时的售价约为1.48万元
𝑎 ^ = 𝑧 − 𝑏 ^ 𝑥≈2+0.363×4.5≈3.63, 故 z 关于 x 的回归直线方程为𝑧 ^ =-0.36x+3.63. 又 z=ln y, 故 y 关于 x 的回归方程为𝑦 ^ =e -0.36x+3.63 . 当 x=9 时,𝑦 ^ =e -0.36×9+3.63=e 0.39 . 因为 ln 1.48≈0.39,所以𝑦 ^ ≈1.48. 故预测某辆 A 型号二手汽车使用年数为 9 年时的售价约为 1.48 万元