
试卷代号:2332 座位号■■ 中央广播电视大学2008一2009学年度第一学期“开放专科”期末考试 高等数学基础试题 2009年1月 题 号 三 四 总 分 分数 得分 评卷人 一、单项选择题(每小题4分,本题共20分) 1.设函数f(x)的定义域为(一∞,十∞),则函数f(x)一f(一x)的图形关于( )对称. A.y=x B.x轴 C.y轴 D.坐标原点 2.当x→0时,下列变量中( )是无穷大量 A.1+2x B.√E x C.0.001 D.2 3.设f(x)在点x=1处可导,则mf1-》二f=(). A.2f(1) B.一f(1) C.f(1) D.-2f(1) 4.函数y=x2一6x一3在区间(2,4)内满足( ). A.先单调下降再单调上升 B.单调上升 C.先单调上升再单调下降 D.单调下降 S.(zcosz-335+1)dr( A.0 B.元 C.2π D.8 1613
试卷代号:2332 座位号巨二」 中央广播电视大学2008-2009学年度第一学期“开放专科”期末考试 高等数学基础 试题 2009年 1月 题 号 四 总 分 分 数 得 分 评卷人 一、单项选择题 (每小题 4分 ,本题共 20分 ) 1.设函数 f (x)的定义域为(-oo,+0),则函数 f(x)- f(-x)的图形关于( A. y = x B. x轴 C. y轴 D.坐标原点 2.当 X-0时 ,下列变量中( )是无穷大量. A. 卫1+丝2兰x B,万 )对称. x ’0.001 D. 2一x 3.设 f (x)在点 x=1处可导,则limf(1-h h)-f(1)一( A. 2f'(1) C. f'(1) 4.函数 y=x2-6x-3在区间(2,4)内满足( A.先单调下降再单调上升 C.先单调上升再单调下降 B. -厂(1) D. -2f(1) B.单调上升 D.单调下降 百(xcosx一3x'+l)d_r( 扣l es J 尸匕 A. 0 B. n C. 27c D.粤 L 1613
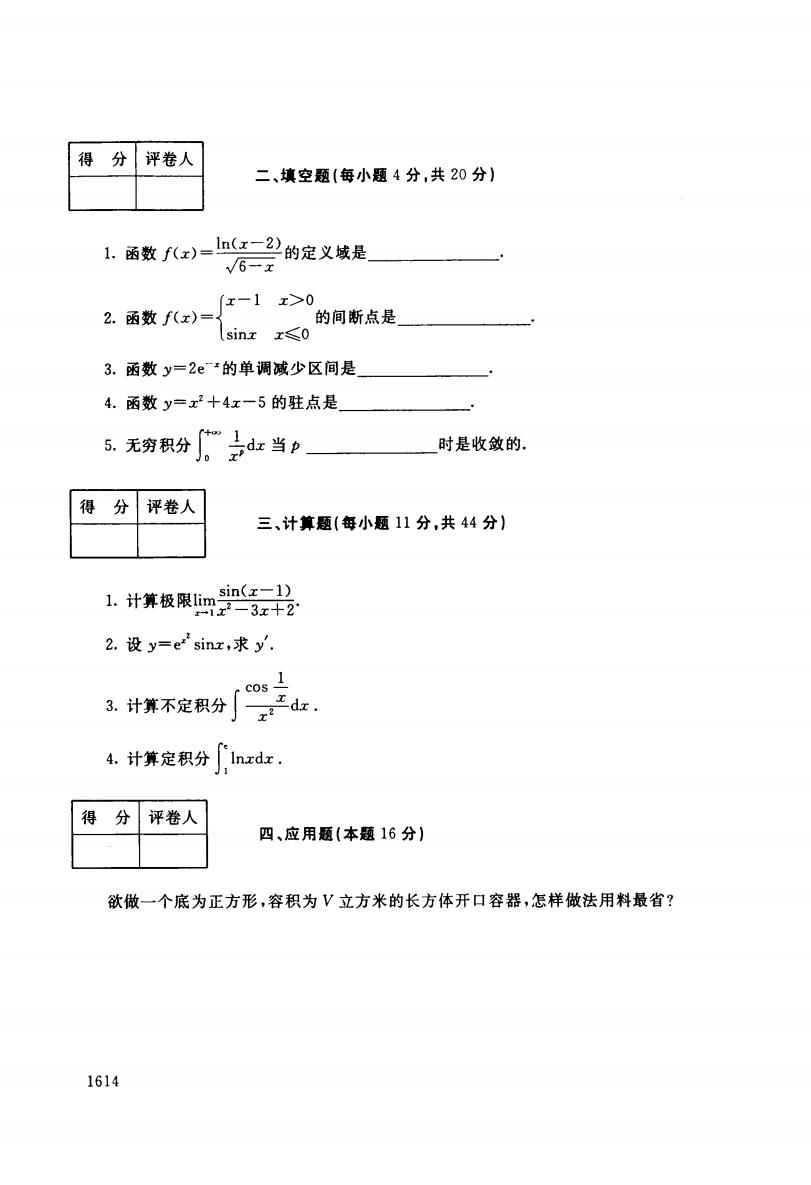
得分 评卷人 二、填空题(每小题4分,共20分)】 1.函数f(x)-lnx一2的定义域是 √6-x x-1x>0 2.函数f(x)= 的间断点是 sinx x≤o 3.函数y=2e的单调减少区间是 4.函数y=x2十4x一5的驻点是 5.无穷积分 d当p 时是收敛的. 得 分 评卷人 三、计算题(每小题11分,共44分) sin(x-1) 1.计算极限m-3z十2 2.设y=e2sinx,求y'. 3.计算不定积分 4.计算定积分 Inzdz. 得 分 评卷人 四、应用题(本题16分) 欲做一个底为正方形,容积为V立方米的长方体开口容器,怎样做法用料最省? 1614
得 分 评卷人 二、填空题 【每小题 4分 .共 20分) 1.函数 f(x) = ln(x一2) 了6一x 的定义域是 2.函,,(二)一{x一 1 x> 0 的间断点是 sinx x毛0 3.函数 y=2e“的单调减少区间是 4.函数y=x' +4x-5的驻点是_ 5.无穷积分厂一步d二当,— 时是收敛的. 得 分 评卷人 三、计算题《每小题 11分.共 44分 ) 1.计算极限lim sin(x一1) 扩 一3x+2' 2.设y=e",sinx,求y 3.计算不定积分 r COs一 I X 」 I一,z ux J X 1 x 4.计算定积分犷lnxdx. 得 分 评卷人 四、应用题(本题 16分) 欲做一个底 为正方形 ,容积为 V立方米的长方体开 口容器 ,怎样做法用料最省? 1614

试卷代号:2332 中央广播电视大学2008一2009学年度第一学期“开放专科”期末考试 高等数学基础试题答案及评分标准 (供参考) 2009年1月 一、单项选择题(每小题4分,本题共20分) 1.D 2.A 3.B 4.A 5.B 二、填空题(每小题4分,本题共20分) 1.(2,6) 2.x=0 3.(-∞,十∞) 4.x=-2 5.>1 三、计算题(每小题11分,共44分】 1.解:lim sin(x-」 sin(x-1)」 i四2=3x+2-i四x-(x-2=-1 2.解:由导数四则运算法则和复合函数求导法则得 y'=(e"sinz)'=(e)'sinz+e(sinz) =e (2)'sinz+ecosx =2 ce sinz十ecosx 3.解:由换元积分法得 cos 1 ∫2x=-∫os=-m+c 4.解:由分部积分法得 lnzd=xint-∫rd(Inz) =e-∫jdr=1
试卷代号:2332 中央广播电视大学2008-2009学年度第一学期“开放专科”期末考试 高等数学基础 试题答案及评分标准 (供参考) 2009年 1月 一、单项选择题《每小题 4分,本题共20分) 1. D 2. A 3. B 4. A 5. B 二、填空题(每小题 4分,本题共 20分》 (2,6) 2. x二 0 3.(一0 ,十00) 4. x= 一 2 5.> 1 三、计算题《每小题 11分,共 44分) 1.解 : sin(x一 1) u.-m ix Z-3a不2=鹭 sin(x一1) (x一 1) (x一 2) = 一 1 11分 2.解:由导数四则运算法则和复合函数求导法则得 y‘一(e.Z sinx)'=(e-')Isinx+e}' (sinx)' =e" (x2)'sinx+e" cosx =2xe" sinx+ex' cosx 11分 3.解 :由换元积分法得 1 r COS一 I 工 」 !- 1- ax J x _一{Cos工d(与 1 ,。 = 一 sin — .十 七 11分 4.解:由分部积分法得 {:lnxdx一‘一{:一丁:xd(lnx) 一e一犷dx一‘ 11分 1615

四、应用题(本题16分) 解:设底边的边长为x,高为y,容器表面积为S,由已知xy=V,y=当 r? 5r+4y=r+4¥=r+y 令S=2z-y-0,解得x=2W是唯一驻点,易知x=2是函数的最小值点,此时有 y四所以当=y=时用料最有 16分 1616
四、应用题(本题 16分) 解:设底边的边长为x,高为,,容器表面积为S,由已知x2 y=V,,一多 S=x2十‘ xy=x2 +4x " xV一十4xV 令、'=2二一4 x V=0,解得二一守2V是唯一驻点,易知二一'2 2V是函数的最小值点,此时有 =擎 乙 ,所以当二=2V ,y= ' ‘2V时用料最省. 16分 1616